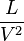MATEMÁTICOS DESDE EL SIGLO XIX HASTA HOY

JOHANN CARL FRIEDRICH GAUSS

Fue un matemático, astrónomo y físico alemán que contribuyó significativamente en muchos campos, incluida la teoría de números, el análisis matemático, la geometría diferencial, la geodesia, el magnetismo y la óptica. Considerado "el príncipe de las matemáticas" y "el matemático más grande desde la antigüedad", Gauss ha tenido una influencia notable en muchos campos de la matemática y de la ciencia, y es considerado uno de los matemáticos que más influencia ha tenido en la historia. Fue de los primeros en extender el concepto de divisibilidad a otros conjuntos.

Gauss fue un niño prodigio de quien existen muchas anécdotas acerca de su asombrosa precocidad siendo apenas un infante, e hizo sus primeros grandes descubrimientos mientras era apenas un adolescente. Completó su magnum opus, Disquisitiones Arithmeticae a los veintiún años (1798), aunque no sería publicado hasta 1801. Un trabajo que fue fundamental para que la teoría de los números se consolidara y ha moldeado esta área hasta los días presentes.

Gauss había deducido la fórmula que da la suma de n términos de una progresión aritmética de la que se conocen el primero y el último término:

JOSEPH LOUIS FRANÇOIS BERTRAND

Joseph Louis François Bertrand (París 11 de marzo de 1822 - 5 de abril de 1900) fue un matemático y economista francés que trabajó en los campos de la teoría de los números, geometría diferencial, cálculo de probabilidades y termodinámica.

Fue profesor en la École Polytechnique y el Collège de France, donde se graduó como ingeniero de minas. También fue miembro de la Academia de Ciencias de París, de la que ocupó el cargo de secretario permanente durante 26 años (1856-1874). El objetó, en 1845, que había al menos un número primo entre n y 2n-2 por cada n > 3. Pafnuti Chebyshov demostró esta conjetura, actualmente llamada postulado de Bertrand, en 1850. También es famoso por una paradoja en el campo de la probabilidad, conocida como la Paradoja de Bertrand.

También tuvo aportaciones en el terreno de la economía. En 1883 publicó una crítica al libro Théorie mathématique de la richesse sociale de Léon Walras, en la que rebatía el proceso de tâtonement argumentando que en la realidad se producen intercambios en situaciones de desequilibrio, razón por la cual cabe considerar la existencia de indeterminación en los precios. También rebatió el principio de maximización de la utilidad con el argumento de que los comerciantes en realidad están interesados principalmente en los beneficios monetarios, no en la utilidad.

En 1838 también revisó la teoría de los monopolios de Antoine Augustin Cournot y consideró que el procedimiento algebraico que utilizó era erróneo. Consideró que los duopolistas compiten en precios en vez de en cantidades, y dedujo un precio final de equilibrio próximo al de la libre competencia.

LEONARDO TORRES QUEVEDO

Leonardo Torres Quevedo (Santa Cruz de Iguña (Molledo), Cantabria, 28 de diciembre de 1852 – Madrid, 18 de diciembre de 1936) fue un ingeniero de Caminos y matemático español de finales del siglo XIX y principios del XX.

Leonardo Torres Quevedo nació el 28 de diciembre, conmemoración de los Santos Inocentes, en 1852, en Santa Cruz de Iguña, Molledo (Cantabria). La familia residía normalmente en Bilbao, donde el padre ejercía de ingeniero de ferrocarriles, aunque también pasaban largas temporadas en el solar materno en La Montaña cántabra. En Bilbao estudió el bachillerato y más tarde fue a París a completar estudios durante 2 años. Por traslado del padre, se instala la familia de Leonardo en Madrid en 1870 y ese mismo año inicia sus estudios superiores en la Escuela Oficial del Cuerpo de Ingenieros de Caminos. Suspende temporalmente sus estudios en 1873 para acudir como voluntario a la defensa de Bilbao, que había sido sitiada por las tropas carlistas durante la Tercera Guerra Carlista. De vuelta a Madrid finalizará sus estudios en 1876 siendo el cuarto de su promoción.

Comienza a ejercer su carrera en la misma empresa de ferrocarriles en la que trabajaba su padre, pero emprende enseguida un largo viaje por Europa para conocer de primera mano los avances científicos y técnicos, sobre todo en la incipiente área de la electricidad. De regreso a España se instala en Santander donde él mismo sufragará sus trabajos e inicia una actividad de estudio e investigación que no abandonará. Fruto de las investigaciones en estos años aparecerá su primer trabajo científico en 1893. En 1885 contrae matrimonio, del que nacerán ocho hijos.

En 1899 se instala en Madrid participando de su vida cultural. De las labores que en estos años llevaba a cabo el Ateneo se creará en 1901 el Laboratorio de Mecánica Aplicada, más tarde de Automática, del que será nombrado director; el Laboratorio se dedicará a la fabricación de instrumentación científica. Ese mismo año ingresa en la Real Academia de Ciencias Exactas, Físicas y Naturales de Madrid, entidad de la que fue presidente en 1910. Entre los trabajos del Laboratorio caben destacar el cinematógrafo de Gonzalo Brañas, el espectrógrafo de rayos X de Cabrera y Costa, el micrótomo y panmicrótomo de Santiago Ramón y Cajal.

En 1916 el rey Alfonso XIII le impone la Medalla Echegaray; en 1918 rechaza el cargo de ministro de Fomento. En 1920 ingresa en la Real Academia Española, en el sillón que había ocupado Pérez Galdós, y pasa a ser miembro de las sección de Mecánica de la Academia de Ciencias de París. En 1922 la Sorbona le nombra Doctor Honoris Causa y, en 1927 se le nombra uno de los doce miembros asociados de la Academia de Ciencias de París.

Fue un decidido partidario del idioma internacional esperanto, que apoyó, entre otros lugares, en el Comité de Cooperación Cultural de la Sociedad de Naciones.

Leonardo Torres Quevedo muere en Madrid, en plena Guerra Civil el 18 de diciembre de 1936, cuando le faltaban 10 días para cumplir 84 años.

SANTIAGO RAMÓN Y CAJAL

Santiago Ramón y Cajal (nacido en Petilla de Aragón (Navarra), el 1 de mayo de 1852 - muerto en Madrid, 17 de octubre de 1934) fue un histólogo español, obtuvo el premio Nobel de Medicina en 1906 por descubrir los mecanismos que gobiernan la morfología y los procesos conectivos de las células nerviosas, una nueva y revolucionaria teoría que empezó a ser llamada la «doctrina de la neurona».

Cursó la carrera de Medicina en Zaragoza,donde toda su familia se trasladó en 1870. Cajal se centró en sus estudios universitarios con éxito y, tras licenciarse en medicina, fue llamado a filas.

El año 1875 marcó también el inicio del doctorado de Cajal y de su vocación científica. Él mismo se costeó su primer microscopio antes de ganar, en 1876, una plaza de practicante en el Hospital Nuestra Señora de Gracia de Zaragoza. Un año después, tras fracasar en varias oposiciones, logró cátedras en distintas facultades de provincia hasta que logró la de Madrid en Histología, donde fue investido doctor. Allí comenzó para Cajal una época de altibajos, con un 1878 terrible, marcado por la enfermedad de la tuberculosis, y un 1879 exitoso, con la obtención de la plaza de Director de Museos Anatómicos de Zaragoza y su boda con Silveria Fañanás García el 19 de julio, con quien tendría siete hijos.

Ganó la cátedra de Anatomía Descriptiva de la Facultad de Medicina de Valencia en 1883, donde pudo estudiar la epidemia de cólera que azotó la ciudad el año 1885. En 1887 se trasladó a Barcelona para ocupar la cátedra de histología creada en la Facultad de Medicina de la Universidad de Barcelona. Fue en 1888, definido por el propio Cajal como su "año cumbre", cuando descubrió los mecanismos que gobiernan la morfología y los procesos conectivos de las células nerviosas de la materia gris del sistema nervioso cerebroespinal

Su teoría fue aceptada en 1889 en el Congreso de la Sociedad Anatómica Alemana, celebrado en Berlín. Su esquema estructural del sistema nervioso como un aglomerado de unidades independientes y definidas pasó a conocerse con el nombre de «doctrina de la neurona», y en ella destaca la ley de la polarización dinámica, modelo capaz de explicar la transmisión unidireccional del impulso nervioso.

En 1892 ocupó la cátedra de Histología e Histoquímica Normal y Anatomía Patológica de la Universidad Central de Madrid. Logró que el gobierno creara en 1902 un moderno Laboratorio de Investigaciones Biológicas en el que trabajó hasta 1922, momento en el que pasa a prolongar su labor en el Instituto Cajal, en donde mantendría su labor científica hasta su muerte.

Entre 1897 y 1904 publicó, en forma de fascículos, su obra magna Histología del sistema nervioso del hombre y de los vertebrados.

Su trabajo y su aportación a la neurociencia se verían reconocidos, finalmente, en 1906, con la concesión del Premio Nobel de Fisiología y Medicina, galardón que compartió con el médico italiano Camillo Golgi, cuyo método de tinción aplicó Cajal durante años. Tras el premio, Cajal aún publicó muchas obras literarias y biográficas y sus Estudios sobre la degeneración del sistema nervioso. Mientras tanto, se consagró a sus alumnos. Ellos fueron quienes le acompañaron, por expreso deseo del propio Cajal, en su último adiós, ocurrido el 17 de octubre de 1934, poco después de publicar su conocida obra El mundo visto a los ochenta años.

TEIJI TAKAGI

Teiji Takagi (, 21 de abril de 1875 - 28 de febrero de 1960) fue un matemático japonés, conocido por comprobar la existencia del teorema de Takagi en la teoría de cuerpos de clases.

Nació en la montañosa región rural de Gifu, Japón. Comenzó con las matemáticas a los 10 años, leyendo textos en inglés, dado que todavía no estaban traducidos al japonés. Después de su asistencia al instituto para estudiantes superdotados y no superdotados, fue a la Universidad de Tokio, en esa época la única universidad del pais. Allí aprendió matemáticas de los "clásicos europeos" como el Álgebra de Salmon y el Lehrbuch der Algeba, de Weber. Ayudado por Hilbert, estudió posteriormente en Göttingen. Aparte de su trabajo en la Teoría de números algebraicos, escribió un gran número de libros de texto japoneses sobre matemáticas y geometría, y fue también colaborador durante la II Guerra Mundial en el desarrollo del sistema de cifrado japonés PURPLE.

ALBERT EINSTEIN

Albert Einstein (14 de marzo de 1879 - 18 de abril de 1955) fue un físico alemán, nacionalizado suizo primero, posteriormente estadounidense. Es el científico más conocido e importante del siglo XX. En 1905, siendo un joven físico desconocido, empleado en la Oficina de Patentes de Berna (Suiza), publicó su Teoría de la Relatividad Especial. En ella incorporó, en un marco teórico simple y con base en postulados físicos sencillos, conceptos y fenómenos estudiados anteriormente por Henri Poincaré y Hendrik Lorentz. Probablemente, la ecuación de la física más conocida a nivel popular es la expresión matemática de la equivalencia masa-energía, E=mc², deducida por Einstein como una consecuencia lógica de esta teoría. Ese mismo año publicó otros trabajos que sentarían algunas de las bases de la física estadística y la mecánica cuántica.

En 1915 presentó la Teoría General de la Relatividad, en la que reformuló por completo el concepto de gravedad. Una de las consecuencias fue el surgimiento del estudio científico del origen y evolución del Universo por la rama de la física denominada cosmología. Muy poco después, Einstein se convirtió en un icono popular de la ciencia alcanzando fama mundial, un privilegio al alcance de muy pocos científicos.

Obtuvo el Premio Nobel de Física en 1921 por su explicación del efecto fotoeléctrico y sus numerosas contribuciones a la física teórica, y no por la Teoría de la Relatividad, pues el científico a quien se encomendó la tarea de evaluarla, no la entendió, y temieron correr el riesgo de que se demostrara errónea posteriormente. En esa época era aún considerada un tanto controvertida por parte de muchos científicos.

Equivalencia masa-energía

El cuarto artículo de aquel año se titulaba Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig y mostraba una deducción de la ecuación de la relatividad que relaciona masa y energía. En este artículo se exponía que "la variación de masa de un objeto que emite una energía L, es:

donde V era la notación de la velocidad de la luz usada por Einstein en 1905.

Esta ecuación implica que la energía E de un cuerpo en reposo es igual a su masa m multiplicada por la velocidad de la luz al cuadrado:

Muestra cómo una partícula con masa posee un tipo de energía, "energía en reposo", distinta de las clásicas energía cinética y energía potencial. La relación masa-energía se utiliza comúnmente para explicar cómo se produce la energía nuclear; midiendo la masa de núcleos atómicos y dividiendo por el número atómico se puede calcular la energía de enlace atrapada en los núcleos atómicos. Paralelamente, la cantidad de energía producida en la fisión de un núcleo atómico se calcula como la diferencia de masa entre el núcleo inicial y los productos de su desintegración, multiplicada por la velocidad de la luz al cuadrado

ANDRÉI NIKOLÁYEVICH KOLMOGÓROV

Andréi Nikoláyevich Kolmogórov (25 de abril de 1903 - 20 de octubre de 1987) fue un matemático ruso que hizo progresos importantes en los campos de la teoría de probabilidad y de la topología. En particular, desarrolló una base axiomática que supone el pilar básico de la teoría de las probabilidades a partir de la teoría de conjuntos. Trabajó al principio de su carrera en lógica constructivista y en la serie de Fourier. También trabajó en turbulencias y mecánica clásica. Asimismo, fue el fundador de la teoría de la complejidad algorítmica.

Kolmogórov trabajó en la Universidad Estatal de Moscú. Estudió con Nikolái Luzin, doctorándose en 1929.

ANDREW WILES

Sir Andrew John Wiles (Cambridge, Inglaterra, 11 de abril de 1953 - ) es un matemático británico. Alcanzó fama mundial en 1993 por la demostración del último teorema de Fermat.

Wiles pudo demostrar el último teorema de Fermat a partir de la conexión, esbozada por Frey, y demostrada por Ken Ribet en 1985, de que una demostración de la llamada Conjetura de Taniyama-Shimura conduciría directamente a una demostración del último teorema de Fermat. En resumen, la conjetura de Taniyama-Shimura establece que cada curva elíptica puede asociarse unívocamente con un objeto matemático denominado forma modular. Si el último teorema de Fermat fuese falso, entonces existiría una curva elíptica tal que no puede asociarse con ninguna forma modular, y por lo tanto la conjetura de Taniyama-Shimura sería falsa. Por lo tanto, Taniyama-Shimura demuestra el último teorema de Fermat.

La demostración de la conjetura de Taniyama-Shimura suponía ya de por sí un reto de suma importancia, ya que constituía uno de los puntos del llamado Programa Langlands, cuyo objetivo consiste en unificar áreas de las matemáticas que aparentemente no tienen relación entre sí. Wiles pasó los 8 años siguientes a la demostración de Ribet en completo aislamiento trabajando en el problema, lo cual es un modo de trabajo inusual en matemáticas, donde es habitual que matemáticos de todo el mundo compartan sus ideas a menudo. Para no levantar sospechas, Wiles fue publicando artículos periódicamente, como haría cualquier matemático de cualquier universidad del mundo.

En 1993, Wiles creyó que su demostración estaba cerrada:

Uno entra en la primera habitación de una mansión y está en la oscuridad. En una oscuridad completa. Vas tropezando y golpeando los muebles, pero poco a poco aprendes dónde está cada elemento del mobiliario. Al fin, tras seis meses más o menos, encuentras el interruptor de la luz y de repente todo está iluminado. Puedes ver exactamente dónde estás. Entonces vas a la siguiente habitación y te pasas otros seis meses en las tinieblas. Así, cada uno de estos progresos, aunque a veces son muy rápidos y se realizan en un solo día o dos, son la culminación de meses precedentes de tropezones en la oscuridad, sin los que el avance sería imposible.

Último teorema de Fermat establece que no existe solución con números enteros para la ecuación: xⁿ + yⁿ = zⁿ si n es un entero más grande que dos.

SRINIVASA AAIYANGAR RAMANUJAN

Srinivāsa Aaiyangār Rāmānujan, (Erode 22 de diciembre de 1887 - Kumbakonam 26 de abril de 1920) fue un matemático indio muy enigmático. De familia humilde, a los siete años asistió a una escuela pública gracias a una beca. Recitaba a sus compañeros de clase fórmulas matemáticas y cifras de π.

A los 12 años dominaba la trigonometría, y a los 15 le prestaron un libro con 6.000 teoremas conocidos, sin demostraciones. Ésa fue su formación matemática básica. En 1903 y 1907 suspendió los exámenes universitarios porque sólo se dedicaba a sus diversiones matemáticas.

En 1912 fue animado a comunicar sus resultados a tres distinguidos matemáticos. Dos de ellos no le respondieron, pero sí lo hizo Godfrey Harold Hardy, de Cambridge. Hardy estuvo a punto de tirar la carta, pero la misma noche que la recibió se sentó con su amigo John Edensor Littlewood (v.) a descifrar la lista de 120 fórmulas y teoremas de Ramanujan. Horas más tarde creían estar ante la obra de un genio. Hardy tenía su propia escala de valoración para el genio matemático: 100 para Ramanujan, 80 para David Hilbert, 30 para Littlewood y 25 para sí mismo. Algunas de las fórmulas de Ramanujan le desbordaron, pero escribió ...forzoso es que fueran verdaderas, porque de no serlo, nadie habría tenido la imaginación necesaria para inventarlas. Invitado por Hardy, Ramanujan partió para Inglaterra en 1914 y comenzaron a trabajar juntos. En 1917 Ramanujan fue admitido en la Royal Society de Londres y en el Trinity College, siendo el primer indio que lograba tal honor. De salud muy débil, moría tres años después.

Hardy escribió de Rāmānujan:

"Los límites de sus conocimientos eran sorprendentes como su profundidad. Era un hombre capaz de resolver ecuaciones modulares y teoremas ...de un modo jamás visto antes, su dominio de las fracciones continuas era...superior a la de todo otro matemático del mundo; ha encontrado por sí solo la ecuación funcional de la función zeta y los términos más importantes de la teoría analítica de los números; sin embargo no había oído hablar jamás de una función doblemente periódica o del Teorema de Cauchy y poseía una vaga idea de lo que era una función de variable compleja..."

Lo principal de los trabajos de Ramanujan está en sus cuadernos, escritos por él en nomenclatura y notación particular, con ausencia de demostraciones, lo que ha provocado una hercúlea tarea de desciframiento y reconstrucción, aún no concluida. Fascinado por el número π, desarrolló potentes algoritmos para calcularlo.

Rāmānujan trabajó principalmente en la teoría analítica de los números y devino célebre por sus numerosas fórmulas sumatorias referidas a las constantes tales como π y la base natural de los logaritmos, los números primos y la función de fracción de un entero obtenida junto a Godfrey Harold Hardy

Aquí se reportan algunos de los hallazgos de Ramanujan, y los resultados obtenidos en colaboración con Hardy a inicios del siglo XX:

Propiedad de los números altamente compuestos
La funciones de partición y sus asintóticas
Función theta de Ramanujan

Ha logrado notables progresos y descubrimientos en las áreas relativas a :

Funciones Gamma

Formas modulares

Series divergentes

Series hipergeométricas

Teoría de los números primos

BIBLIOGRAFÍA

1. http://centros5.pntic.mec.es/~barriope/matematicas/web_taller_0203/mujeres/monica/teano.htm
2. http://wikipedia.com
3. http://personal.redestb.es/javfuetub/biografias/mujmat.htm

MUJERES MATEMÁTICAS

TEANO

Teano nació en Crotona, fue discípula de Pitágoras y se casó con él. Enseñó en la escuela pitagórica. Se conservan fragmentos de cartas y escritos que prueban que fue una mujer que escribió mucho, y eso mismo le atribuye la tradición, , que considera como suyos varios tratados de matemáticas, física y medicina. El tratado Sobre la Piedad del que se conserva un fragmento con una reflexión sobre el número se piensa que es de Teano. Se le atribuyen otros tratados sobre los poliedros regulares y sobre la teoría de la proporción, en particular sobre la proporción áureaDespués de la rebelión contra el gobierno de Crotona, a la muerte de Pitágoras, Teano pasó a dirigir la comunidad, con la escuela destruida y sus miembros exiliados y dispersos, sin embargo con la ayuda de dos de sus hijas difundió los conocimientos matemáticos y filosóficos por Grecia y por Egipto.

HIPATIA

Nació en Alejandría, su padre era matemático y profesor de museo y se preocupó de darle una buena formación y lo consiguió pues Hipatia fue una filósofa, astrónoma y matemática que llegó a superar a su padre.
Contribuyó a la invención de aparatos como el aerómetro y construyó el astrolabio.

Era defensora del heliocentrismo (teoría que defiende que la tierra gira alrededor del sol).

Trabajó sobre escritos relacionados con las ecuaciones diofánticas, sobre las cónicas y la geometría y también elaboró tablas sobre movimientos de los astros.

Estudió en el museo y después viajó por Italia y Atenas donde perfeccionó sus conocimientos, y cuando volvió a Alejandría fue profesora durante 20 años. Enseñó matemáticas, astronomía, lógica, filosofía, mecánica... de todas partes del mundo llegaban estudiantes para aprender de ella.

Hipatia era el símbolo del ideal griego porque reunía sabiduría, belleza, razón y pensamiento filosófico y además era una mujer científica y con papel político importante. En el año 415 cuando tenia 45 años fue asesinada por monjes fanáticos de la iglesia de San Cirilo de Jerusalén ya que ella era partidaria del racionalismo científico griego y no quiso convertirse al cristianismo.

ÉMILIE DE CHÂTELET

Con diez años ya había estudiado matemáticas y la metafísica; a los 12 sabía inglés, italiano, español y alemán y traducía textos en latín. En un café de París no la dejaron entrar por ser mujer. Estudió a Descartes, Leibniz y a Newton. Escribió las instituciones de la física, libro que contiene el cálculo infinitesimal. Hacia 1745 tradujo los principios de la matemática de Newton. Después de quedarse embarazada terminó la edición de la Principia.




MARÍA GAETANA AGNESI

María estudió y en 1738 le publicaron Propositiones philosophicae que abordaba los problemas de filosofía natural que habitualmente se discutían en los salones. Después escribió el libro Instituciones analíticas al uso de la juventud italiana en el que explicaba una parte novedosa de las matemáticas: el calculo analítico. El libro tuvo muy buena crítica.

Se dedicó en profundidad al estudio del álgebra y la geometría y nueve años más tarde aparecieron publicadas las Instituzioni Analitiche, sin duda la obra más importante de toda su carrera como matemática. Fue editado en varios idiomas y se utilizó como manual universitario en las universidades de distintos países, siendo aún cincuenta años más tarde el texto matemático más completo. Se encargó en Italia de los cursos de su padre, convirtiéndose así en la primera mujer de la historia que había dado clase de matemáticas en la universidad.

SOPHIE GERMAIN

Nació el 1-04-1776. Hija de un rico comerciante francés. Se llegó a obsesionar con el estudio de las matemáticas, tanto que su padre, para impedirle que estudiase por las noches le escondia las velas. Con el tiempo sus padres cedieron y financiaron los estudios de su hija.

En esta época la sociedad era muy machista y la mujer no podía dedicarse a tareas usualmente de hombres. Como Sophie no podía ingresar en la École Polytechnique, asumió la identidad de un antiguo alumno (Monsieur Antoine-August Le Blanc). La secretaría de la escuela le enviaba por correo los apuntes y problemas y respondía las soluciones por correo. Al cabo de unos meses el encargado de curso, Lagrange, admirado por la brillantez de las respuestas, solicitó una entrevista con el alumno. Sophie se vió obligada a revelar su auténtica identidad. Lagrage se convirtió en su mentor y amigo.

Sophie admiraba a Gaüs, le escribió, haciéndose pasar por Le Blanc, comunicándole sus descubrimientos matemáticos. Cuando Napoleón invadió Prusia, Sophie, que era amiga de un general de Napoleón que estaba en Prusia, envió un mensaje a su amigo para que garantizase la vida de Gaüs. El general comunicó a Gaüs que debía su vida a mademoiselle Germain. Gaüs quedó agradecido pero sorprendido, pues no conocía a tal señorita. En la próxima carta de Sophie a Gaüs, le reveló su verdadera identidad.

Sophie murió de cáncer de mama. En el certificado de defunción consta como renttiére-annuitant (mujer sin oficio). Más aún, cuando se erigió la torre Eiffel (para la Expo de 1889), se inscribieron los nombres de 72 sabios franceses y Sophie Germain no figura entre ellos.



EMMY AMALIE NOETHER

Nació en 1882 en Erlangen, Alemania y murió en 1935 en Pennsylvania, USA.

Su padre era profesor de matemáticas en Erlangen.

Estudió Frances e Ingles y aunque obtuvo el título de profesora de Ingles y Francés no llegó a ejercer en estas materias.

Se dice que ha sido la matemática más grande de la historia de las matemáticas. Tuvo que vencer muchas dificultades para estudiar matemáticas, porque en ese tiempo a las mujeres no se les permitía estudiar, oficialmente, en las universidades alemanas. Cuando se doctoró en la Universidad de Erlangen (1898) el senado académico declaró que la admisión de mujeres estudiantes "subvertía todo el orden académico".

En 1915 Hilbert y Klein invitaron a Noether a volver a Göttingen y lucharon contra las autoridades universitarias para habilitar como profesora a Noether. No lo consiguieron hasta 1919.

Es famosa por sus trabajos sobre teoría de ideales. En 1921 publicó un artículo (Idealtheorie in Ringbereichen) sobre teoría de anillos tan importante que, desde entonces, se llaman anillos noetherianos a una determinada clase de anillos.

También fue una excelente profesora. Siempre estaba rodeada de estudiantes. In 1933 los nazis, provocaron su expulsión de Göttingen, porque era judía. Se fue a USA.

JULIA ROBINSON

Julia Hall Bowman Robinson (8 de diciembre de 1919 — † 30 de julio de 1985 fue una matemática estadounidense, nacida en San Luis Missouri. Hizo sus estudios universitarios en la Universidad de California, Berkeley, recibiendo el doctorado en 1948. En 1976 fue elegida miembro de la división de matemáticas de la Academia Nacional de Ciencias de Estados Unidos, siendo la primera mujer que obtuvo ese cargo. En 1982 la Asociación de Mujeres en Matemáticas (AWM, por sus siglas en inglés) le dedicó la Conferencia Noether, evento anual destinado a honrar a mujeres que hayan realizado contribuciones fundamentales a la matemática. En 1983 se le concedió un premio McArthur, beca para respaldar el trabajo de científicos del más alto nivel, dotada con medio millón de dólares. Fue presidenta de la Sociedad Americana de Matemáticas (AMS por sus siglas en inglés), la primera mujer con esa responsabilidad. Murió de leucemia en Oakland, California, a los 65 años.

Se la conoce sobre todo por su trabajo en ecuaciones diofánticas y en decidibilidad, que contribuyó en gran medida a la demostración por Yuri Matiyasevich de la irresolubilidad del décimo problema de Hilbert (Teorema de Matiyasevich). De hecho, Robinson sólo se apartó de este campo (ecuaciones diofánticas y decidibilidad) en dos ocasiones: una fue su tesis doctoral, dedicada a la resolubilidad e irresolubilidad de problemas matemáticos; otra, su importante aportación a la teoría de juegos.

Se casó en 1941 con el también matemático Raphael Robinson. Su hija mayor, Constance Reid, es una conocida biógrafa de matemáticos; en particular, por supuesto, de su madre.